Hasse diagram

In order theory, a branch of mathematics, a Hasse diagram ( /ˈhæsə/; German: /ˈhasə/) is a type of mathematical diagram used to represent a finite partially ordered set, in the form of a drawing of its transitive reduction. Concretely, for a partially ordered set (S, ≤) one represents each element of S as a vertex in the plane and draws a line segment or curve that goes upward from x to y whenever y covers x (that is, whenever x < y and there is no z such that x < z < y). These curves may cross each other but must not touch any vertices other than their endpoints. Such a diagram, with labeled vertices, uniquely determines its partial order.

Hasse diagrams are named after Helmut Hasse (1898–1979); according to Birkhoff (1948), they are so-called because of the effective use Hasse made of them. However, Hasse was not the first to use these diagrams; they appear, e.g., in Vogt (1895). Although Hasse diagrams were originally devised as a technique for making drawings of partially ordered sets by hand, they have more recently been created automatically using graph drawing techniques.[1]

The phrase "Hasse diagram" may also refer to the transitive reduction as an abstract directed acyclic graph, independently of any drawing of that graph, but this usage is eschewed here.

Contents

Examples

A "good" Hasse diagram

Although Hasse diagrams are simple as well as intuitive tools for dealing with finite posets, it turns out to be rather difficult to draw "good" diagrams. The reason is that there will in general be many possible ways to draw a Hasse diagram for a given poset. The simple technique of just starting with the minimal elements of an order and then adding greater elements incrementally often produces quite poor results: symmetries and internal structure of the order are easily lost.

Subsets

The following example demonstrates the issue. Consider the powerset 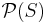\mathcal{P}(S) of the set S = {a, b, c, d}, i.e. the set of all subsets of S, ordered via subset inclusion 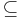\subseteq. Below are three different Hasse diagrams for this partial order (Note that each subset S’ has a node labeled with a 1-0 encoding of whether each of the four elements is ('1') or isn't ('0') in S’.):

       

The leftmost diagram makes clear that the powerset is a graded poset. The middle diagram has the same graded structure, but by making some edges longer than others, it emphasizes a construction of the powerset as a union of two three-dimensional cubes: the vertices in the lower (left) cube represent subsets that do not contain some particular element (say d) of S, while those in the upper (right) cube represent the subsets that do contain d. The rightmost diagram shows some of the internal symmetry of the structure.

Partitions

The following Hasse diagrams also show a 4 element set's partitions, ordered by the refinement relation. The diagram on the left emphasizes that the partitions 1...5 form a sublattice. The whole lattice is not simply a doubled sublattice like in the hypercube example above. The second diagram is reflectionally symmetrical. The edges in the middle would all be vertical lines, but to make them discriminable, they are drawn slightly curved. The third diagram emphasizes the rank structure of the lattice. All elements with the same rank are in the same level of the Hasse diagram, but most of the symmetry is lost.

       

Upward planarity

If a partial order can be drawn as a Hasse diagram in which no two edges cross, its covering graph is said to be upward planar. A number of results on upward planarity and on crossing-free Hasse diagram construction are known:

Notes

  1. ^ E.g., see Di Battista & Tamassia (1988) and Freese (2004).
  2. ^ Garg & Tamassia (1995a), Theorem 9, p. 118; Baker, Fishburn & Roberts (1971), theorem 4.1, page 18.
  3. ^ Garg & Tamassia (1995a), Theorem 15, p. 125; Bertolazzi et al. (1993).
  4. ^ Garg & Tamassia (1995a), Corollary 1, p. 132; Garg & Tamassia (1995b).
  5. ^ Chan (2004).
  6. ^ Jünger & Leipert (1999).

References

External links

Weisstein, Eric W., "Hasse Diagram" from MathWorld.